Suppose you wanted to know whether a change to your product results in impacts to a metric describing your users. The change could be design-related or a new feature, and the impact you want to measure could be purchases, lifetime value, subscription value, or any other possible metric. How do you determine whether the impacts of the change were statistically significant?
This article assumes the reader understands some basic concepts of A/B testing. The below fictitious data shows the subscription value of two sets of customers. After the release of a new product feature to one set of customers, we want to find out whether that change had any impact on the subscription value.
We will use a two sample t-test in this case, which is a statistical method to establish that the values of two variables are different from one another. One of the great things about t-tests is that the standard deviation does not need to be known. However, there are several key assumptions about the data that need to be satisfied:
- Each observation of the variable is independent of the other observations.
- The data is collected from a representative, randomly selected portion of the total population.
- The data follows a normal distribution, allowing us to specify a level of probability (p-value or alpha) as a criterion of acceptance.
- The two variables we are testing have the same variance (as though the distribution for the control group were merely shifted over to become the distribution for the test group, without changing shape). However, there is an adaptation of the t-test that allows for us to deal with variables with differing variances.
In our case, the subscription value of one customer should not have any effect on the subscription value of another customer, meaning we meet the first assumption.
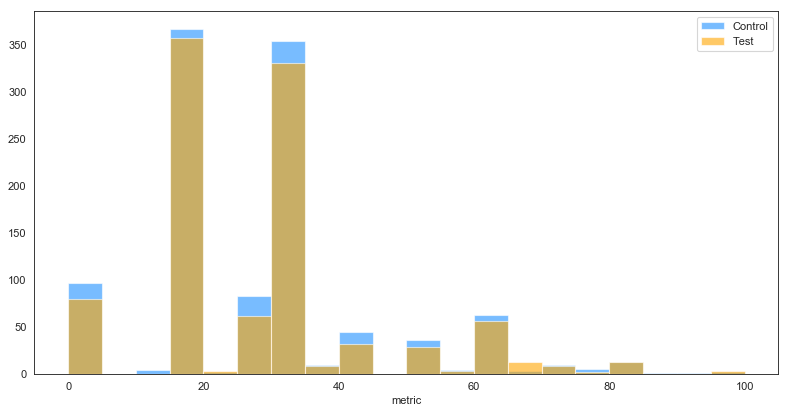
The second and third assumptions can be both met using a single solution. As we can see from Figure 1, our data does not follow a normal distribution. However, we can use a method called bootstrapping to set up our hypothesis test. Bootstrapping is basically random sampling with replacement, and it works because most samples, if randomly chosen, look similar to the population they came from. Thus, even though we are sampling from a sample of the population, we can still get a probability distribution of the statistic in question. We call this probability distribution the sampling distribution. Furthermore, the Central Limit Theorem states a sampling distribution of sample means approximates a normal distribution regardless of the underlying distribution. As a general rule of thumb, samples sizes of 30 or greater are considered sufficient for this Theorem to hold.
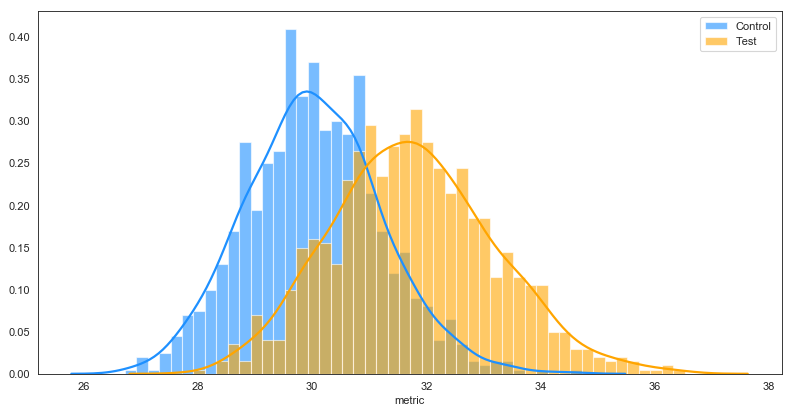
Finally, we find that our variables do not have the same variance, meaning the fourth assumption is not met. However, we can use an adaptation of the t-test, called the Welch’s t-test, which can be used for variables with different variances.

Now that we have our test set up, we will use the ttest_ind function from scipy, specifying equal_var = False in order to perform a Welch’s t-test. The null hypothesis here is that two independent samples have identical expected values. If we receive a p-value of less than 0.05, then we will be able to reject this null hypothesis with confidence.

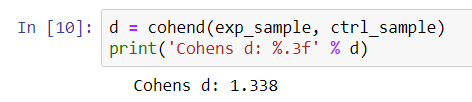
We see that the p-value is very small, meaning we can reject the null hypothesis and conclude the means of the two samples are not equal. To add some flavor to the analysis, we can also size the difference using Cohen’s D value, which is an effect size used to indicate the standardised difference between two means. As a rule of thumb, one could interpret Cohen’s D as follows:
- Small effect = 0.2
- Medium effect = 0.5
- Large effect = 0.8
Note that large effects aren’t necessarily better than small effects. Depending on the context, even small effects may make major impacts to the business. In our context, we see that the calculated Cohen’s D value is 1.338, qualifying it as a “large” effect.